텐서플로우의 예제를 통해서 매우 간단한 뉴럴 네트워크를 알아 봅시다.
앞서 접해본 [TensorFlow] 001. 맛보기와 내용이랑 유사합니다.
둘 다 y = ax + b 일 때, a와 b를 구하는 방법입니다.
하지만 이 예제의 경우, 구해야 하는 a, b를 weights라는 matrix(2x1) 변수로 선언하고, 임의의 표준정규분포 값을 받아서 그 값에서 a와 b를 유추하는 방식으로 진행됩니다.
아! 그리고 도표를 그리기 시작했습니다. 데이터를 인포그래픽으로 보는 일은 즐거운 일입니다.
weights(b, a) 구하기
y = ax + b
학습 데이터로 x와 y가 주어졌을때, 가중치(weights)로 할당되어 있는 a와 b의 최적의 값을 구해 봅시다.
CODE
A simple neural network
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
num_examples = 50
# -2에서 4까지, -6에서 6까지 50(num_examples)단계로 꾸준히 증가하는 값을 받아서 2개의 배열로 저장 (직선 상태)
X = np.array([np.linspace(-2, 4, num_examples), np.linspace(-6, 6, num_examples)])
# 꾸준히 증가하는 X 배열에 표준정규분포 값을 각각 넣어줌 (데이터 분산 발생)
X += np.random.randn(2, num_examples)
x, y = X
# x 배열 값에 1을 붙여서 x_with_bias 생성 (1을 붙인 이유는 가중치(weights에서 b, a를 사용할 때, b를 그대로 보존하기 위함) y = b*1 + ax = ax + b
x_with_bias = np.array([(1., a) for a in x]).astype(np.float32)
losses = []
training_steps = 50
learning_rate = 0.002
with tf.Session() as sess:
# 입력은 x_with_bias(50x2) 사용
input = tf.constant(x_with_bias)
# 타겟은 y를 전치행렬(1x50 → 50x1) 설정
target = tf.constant(np.transpose([y]).astype(np.float32))
# 가중치 출력 텐서의 모양은 (2x1)으로 정규분포의 분산 0, 표준편차 0.1을 가지는 임의의 값을 초기값으로 설정
weights = tf.Variable(tf.random_normal([2, 1], 0, 0.1))
# 모든 텐서 변수 초기화
tf.initialize_all_variables().run()
# input(50x2)과 가중치 값(2x1)을 matrix multiple = yhat은 (50x1) 값이 됨, yhat = 학습 진행중인 데이터
yhat = tf.matmul(input, weights)
# yhat(50x1)에서 target(50x1) 값을 뺀 값을 yerror로 설정
yerror = tf.sub(yhat, target)
# 학습중인 weights와 실제 target의 차이의 손실값의 평균 (평균 - reduce_mean)
loss = tf.reduce_mean(tf.nn.l2_loss(yerror))
# 경사하강법으로 loss가 최소값이 되도록 학습 설정
update_weights = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
# 50회 학습
for _ in range(training_steps):
# 반복적으로 경사하강법을 통해 텐서플로우 변수들을 업데이트 함
update_weights.run()
losses.append(loss.eval())
# 학습이 종료되면 결과 값을 출력
betas = weights.eval()
yhat = yhat.eval()
# 그래프로 표현
# fig는 도표를 그릴 영역을 의미함. 도표가 1x2 형태로 가로로 2개 들어감
fig, (ax1, ax2) = plt.subplots(1, 2)
# 도표간 거리는 0.3
plt.subplots_adjust(wspace=.3)
# 그릴 영역의 사이즈는 가로 10, 세로 4
fig.set_size_inches(10, 4)
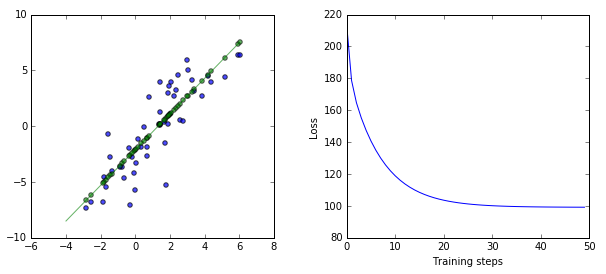
# 첫번째 도표(ax1)에 입력에 따른 출력 값을 2차원 평면에 점으로 찍음
ax1.scatter(x, y, alpha=.7)
# 첫번째 도표(ax1)에 최종 가중치(weights)를 적용했을 때, 예상되는 target 값을 기준으로 2차원 평면에 점으로 찍음
ax1.scatter(x, np.transpose(yhat)[0], c="g", alpha=.6)
line_x_range = (-4, 6)
# 첫번째 도표(ax1)에 x 값 -4에서 6사이에서 최종 가중치(weights)에 따른 직선 그래프를 그림 betas[0]은 b를 의미 betas[1]은 a를 의미 (yhat = b + a*input)
ax1.plot(line_x_range, [betas[0] + a * betas[1] for a in line_x_range], "g", alpha=0.6)
# 두 번째 도표(ax2)에 학습 진행에 따른 losses를 도식화)
ax2.plot(range(0, training_steps), losses)
ax2.set_ylabel("Loss")
ax2.set_xlabel("Training steps")
plt.show()
Result
요약
y = ax + b 인 상황에서, 입력값 x(input)와 출력값 y(target)을 알고 있다. 이때 최적의 a와 b를 구해보자.
예를 들어 위와 같이 input(coefficient), target(constant) 값이 주어졌을때, x, y를 찾을 수 있다.
하지만, 표준정규분포에 의한 input과 target에 대하여 가장 근접 수렴하는 x, y 값을 찾고자 할 때, 학습(training)을 통해서 최적의 값을 찾을 수 있다.
이때 위 도표의 x와 y를 가중치(weights)로 가져가기 위해서는 y=ax+b에 준하는 행렬(matrix)을 설정해주면 됨. 따라서, b 값을 온전히 보전하기 위해 1을 이용함.
- 아래 예와 같이 좌측 행렬 5, 1 들어간 부분이 전부 1이 들어간 형태이고, x는 b(offset), y는 a(기울기)
- 하지만 위와 같은 예와 같이 명확히 값이 떨어지지 않는 이유는, matrix(행렬) 입력(input)과 출력(target)이 명확한 수치가 아니라, 분산 값으로 인해서 표준정규분포 값이기 때문임. (Line 10)
- 그래서 모든 샘플(exaplmes)에 대하여 가장 수렴할 수 있는 a와 b 값을 찾기 위해서 학습을 해 나가는 과정이 필요함.
- 학습이 전개될 때마다 a와 b의 값(weights 2x1 )을 업데이트 시키는데 경사하강법으로 loss가 최소가 되도록 학습을 진행해 나간다.
위 변수와 OP 의미 분석
input
- constant 타입 : (50x2) 행렬 ( -2 ~ 4 까지 데이터를 균등하게 50개로 쪼개 놓은 값에 표준정규분포 데이터 합산하고 1열의 값을 모두 1로 놓음
- input 데이터의 형태가 [1, x] 형태인 이유?
- y(target) = ax(input.x) + 1b(input.1) : b를 온전히 보전하기 위해서 1을 사용
weights
- variable 타입 : (2x1) 행렬로 값으로 정규분 포분산 0, 표준편차 0.1을 가지는 임의의 값으로 초기 세팅
target
- constant 타입 : (50x1) 행렬 초기 분산 데이터 50개가 들어있다. ( -6 ~ 6 까지 데이터를 균등하게 50개로 쪼개 놓은 값에 표준정규분포 데이터 합산)
yhat
- 각각의 행렬 input(50x2), weight(2x1)을 곱한 값을 만듬 (50x1)
yerror
- yhat(학습중인 값(50x1)에 target 데이터(50x1)과의 차이가 얼마나 나는지에 대한 에러 값을 구함
loss
- L2 loss로 reduce_mean... loss 평균을 줄여나간다 의미 같음 (앞으로 자주 만날듯..... 좀 더 지켜보기로)
update_weights
- operator 타입 : 경사하강법으로 loss가 최소가 되도록 학습을 진행. 학습에서 필요한 변수(weights가 학습을 통해서 계속 변경됨)
learning_rates
- constant 타입 : 왜 학습 비율이 0.002인가? 이 값이 가지는 진정한 의미는 무엇인가?... 이 비율이 적용되는 기준이 무엇인지는 확인이 필요할 것 같음.
plt
- plot의 개념으로 보임. fig는 전체 그리는 영역, subplot은 그려지는 도표의 개수를 의미하는 것 같음.
- scatter는 값을 점 단위로 그리는 듯 함
- yhat scatter와 직선 곡선 그래프는 확인 필요
궁금한 점
- 로스를 구하는 이유
- 경사하강법이란?